「CS61B」Note(1) HW2 Percolation
In this program, the task is to write a program to estimate the value of the percolation threshold via Monte Carlo simulation.
Percolation.java
Percolation data type. To model a percolation system, create a data type in the hw2 package named Percolation with the following API:
public class Percolation {
public Percolation(int N) // create N-by-N grid, with all sites initially blocked
public void open(int row, int col) // open the site (row, col) if it is not open already
public boolean isOpen(int row, int col) // is the site (row, col) open?
public boolean isFull(int row, int col) // is the site (row, col) full?
public int numberOfOpenSites() // number of open sites
public boolean percolates() // does the system percolate?
public static void main(String[] args) // use for unit testing (not required)
}
If we want to check isFull() and percolates(), we could call connected of WeightedQuickUnionUF for each item in top row, but too slow. It will cost linear time. So the solution is to create a virtual top site connected to all open items in top row and a similar virtual site at bottom: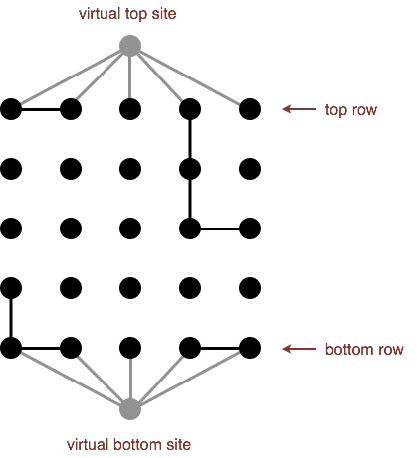 
The implementation is as follows:
public class PercolationOriginal {
private int side_length;
private int numberOfSites;
private WeightedQuickUnionUF quickUnion;
private boolean[] isOpenList;
private int numberOfOpenSites_;
public PercolationOriginal(int N) throws java.lang.IllegalArgumentException{ // create N-by-N grid, with all sites initially blocked
if (N < 1){
throw new java.lang.IllegalArgumentException("Error:The side length must be at least 1");
}
side_length = N;
numberOfSites = N * N + 2;
isOpenList = new boolean[numberOfSites - 2]; // default values of boolean arrays created by 'new boolean[]' method are null
numberOfOpenSites_ = 0;
quickUnion = new WeightedQuickUnionUF(numberOfSites);
}
private int map2Dto1D(int row, int col){
return side_length * row + col;
}
public void open(int row, int col) throws java.lang.IndexOutOfBoundsException{ // open the site (row, col) if it is not open already
if (row > side_length - 1 || col > side_length - 1 || row < 0 || col < 0){
throw new java.lang.IndexOutOfBoundsException("Error:The index is out of bounds:0-" + (side_length - 1));
}
int index = map2Dto1D(row, col);
if (isOpen(row, col)) { return; } else {
isOpenList[index] = true;
numberOfOpenSites_ += 1;
}
if (row - 1 == -1) { //
quickUnion.union(index, numberOfSites - 2); // Use the numberOfSites - 2(second-to-last) element of quickUnion to represent top virtual site
} else if (isOpen(row - 1, col)) {
quickUnion.union(index, map2Dto1D(row - 1, col));
}
if (row + 1 == side_length) {
quickUnion.union(index, numberOfSites - 1); // Use the numberOfSites - 1(last) element of quickUnion to represent bottom virtual site
} else if (isOpen(row + 1, col)) {
quickUnion.union(index, map2Dto1D(row + 1, col));
}
if (col - 1 >= 0 && isOpen(row, col - 1)) {
quickUnion.union(index, map2Dto1D(row, col - 1));
}
if (col + 1 <= side_length - 1 && isOpen(row, col + 1)) {
quickUnion.union(index, map2Dto1D(row, col + 1));
}
}
public boolean isOpen(int row, int col) throws java.lang.IndexOutOfBoundsException{ // is the site (row, col) open?
if (row > side_length - 1 || col > side_length - 1 || row < 0 || col < 0){
throw new java.lang.IndexOutOfBoundsException("Error:The index is out of bounds:0-" + (side_length - 1));
}
return isOpenList[map2Dto1D(row, col)];
}
public boolean isFull(int row, int col) throws java.lang.IndexOutOfBoundsException{ // is the site (row, col) full?
if (row > side_length - 1 || col > side_length - 1 || row < 0 || col < 0){
throw new java.lang.IndexOutOfBoundsException("Error:The index is out of bounds:0-" + (side_length - 1));
}
return quickUnion.connected(map2Dto1D(row, col), numberOfSites - 2);
}
public int numberOfOpenSites() { // number of open sites
return numberOfOpenSites_;
}
public boolean percolates() { // does the system percolate?
return quickUnion.connected(numberOfSites - 1, numberOfSites - 2);
}
But there is a potential downside of these virtual sites which is backwash. Water should not flow back up through the virtual bottom site: 
To solve the problem, we need to creat a new quickUnion without bottom site, update it simultaneously with the old quickUnion, and use it to judge isFull(). For other methods(isOpen(), percolates()), we still use the quickUnion with bottom site to speed things up.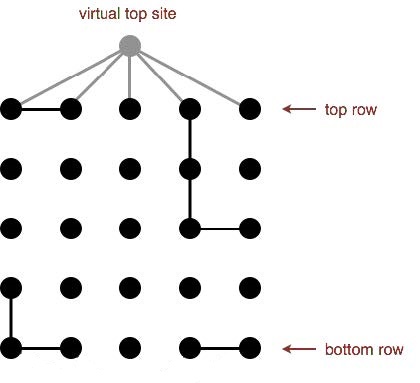 
Then after the system percolates, water will not flow back up again: 
The new implementation of Percolation with a second WeightedQuickUnionUF is as follow:
public class Percolation {
private int side_length;
private int numberOfSites;
private WeightedQuickUnionUF quickUnion;
private WeightedQuickUnionUF quickUnionNew; // create a quickUnion Without Bottom Site
private boolean[] isOpenList;
private int numberOfOpenSites_;
public Percolation(int N) throws java.lang.IllegalArgumentException{ // create N-by-N grid, with all sites initially blocked
if (N < 1){
throw new java.lang.IllegalArgumentException("Error:The side length must be at least 1");
}
side_length = N;
numberOfSites = N * N + 2;
isOpenList = new boolean[numberOfSites - 2]; // default values of boolean arrays created by 'new boolean[]' method are null
numberOfOpenSites_ = 0;
quickUnion = new WeightedQuickUnionUF(numberOfSites);
quickUnionNew = new WeightedQuickUnionUF(numberOfSites - 1); // Create a new quickUnion without bottom virtual site to solve backwash
}
private int map2Dto1D(int row, int col){
return side_length * row + col;
}
public void open(int row, int col) throws java.lang.IndexOutOfBoundsException{ // open the site (row, col) if it is not open already
if (row > side_length - 1 || col > side_length - 1 || row < 0 || col < 0){
throw new java.lang.IndexOutOfBoundsException("Error:The index is out of bounds:0-" + (side_length - 1));
}
int index = map2Dto1D(row, col);
if (isOpen(row, col)) { return; } else {
isOpenList[index] = true;
numberOfOpenSites_ += 1;
}
if (row - 1 == -1) {
quickUnion.union(index, numberOfSites - 2);
quickUnionNew.union(index, numberOfSites - 1 - 1); // In the new quickUnion, use last element to represent top virtual site
} else if (isOpen(row - 1, col)) {
quickUnion.union(index, map2Dto1D(row - 1, col));
quickUnionNew.union(index, map2Dto1D(row - 1, col));
}
if (row + 1 == side_length) {
quickUnion.union(index, numberOfSites - 1);
} else if (isOpen(row + 1, col)) {
quickUnion.union(index, map2Dto1D(row + 1, col));
quickUnionNew.union(index, map2Dto1D(row + 1, col));
}
if (col - 1 >= 0 && isOpen(row, col - 1)) {
quickUnion.union(index, map2Dto1D(row, col - 1));
quickUnionNew.union(index, map2Dto1D(row, col - 1));
}
if (col + 1 <= side_length - 1 && isOpen(row, col + 1)) {
quickUnion.union(index, map2Dto1D(row, col + 1));
quickUnionNew.union(index, map2Dto1D(row, col + 1));
}
}
public boolean isOpen(int row, int col) throws java.lang.IndexOutOfBoundsException{ // is the site (row, col) open?
if (row > side_length - 1 || col > side_length - 1 || row < 0 || col < 0){
throw new java.lang.IndexOutOfBoundsException("Error:The index is out of bounds:0-" + (side_length - 1));
}
return isOpenList[map2Dto1D(row, col)];
}
public boolean isFull(int row, int col) throws java.lang.IndexOutOfBoundsException{ // is the site (row, col) full?
if (row > side_length - 1 || col > side_length - 1 || row < 0 || col < 0){
throw new java.lang.IndexOutOfBoundsException("Error:The index is out of bounds:0-" + (side_length - 1));
}
return quickUnionNew.connected(map2Dto1D(row, col), numberOfSites - 1 - 1); // Use new quickUnion to check isFull
}
public int numberOfOpenSites() { // number of open sites
return numberOfOpenSites_;
}
public boolean percolates() { // does the system percolate?
return quickUnion.connected(numberOfSites - 1, numberOfSites - 2);
}
PercolationStats.java
Monte Carlo simulation. To estimate the percolation threshold, consider the following computational experiment:
- Initialize all sites to be blocked.
- Repeat the following until the system percolates:
- Choose a site uniformly at random among all blocked sites.
- Open the site.
- The fraction of sites that are opened when the system percolates provides an estimate of the percolation threshold.
public class PercolationStats {
private int N;
private int T;
private Percolation p1;
private double[] threshold;
public PercolationStats(int N, int T, PercolationFactory pf){ // perform T independent experiments on an N-by-N grid
this.N = N;
this.T = T;
threshold = new double[T];
for (int i = 0; i < T; i++) {
p1 = pf.make(N);
while(!p1.percolates()) {
int siteIndex = StdRandom.uniform(N * N);
p1.open(siteIndex / N, siteIndex % N);
}
threshold[i] = (double)p1.numberOfOpenSites() / (N * N);
}
}
public double mean(){ // sample mean of percolation threshold
return StdStats.mean(threshold);
}
public double stddev() { // sample standard deviation of percolation threshold
return StdStats.stddev(threshold);
}
public double confidenceLow() { // low endpoint of 95% confidence interval
return StdStats.mean(threshold);
}
public double confidenceHigh() { // high endpoint of 95% confidence interval
return mean() + 1.96 * stddev() / Math.sqrt(T);
}
}
