「CS61B」Note(2) HW3 Hashing

This homework helps us get better understanding of hash tables, which I have been struggled with a little bit. The requirements are at this link.

Equals

First task is to overide equals method in SimpleOomage. Just make sure that all red, green and blue are equal, and consider is self and null situation.

@Override
public boolean equals(Object o) {
    // TODO: Write this method.
    if (o == this) { return true; }
    if (o == null) { return false; }
    if (o.getClass() != this.getClass()) return false;
    SimpleOomage that = (SimpleOomage) o;
    return (this.red == that.red) && (this.green == that.green) && (this.blue == that.blue);
}

Hashcode

Also, we need to overide hashcode. The Java specification for equals mentions this:

Note that it is generally necessary to override the hashCode method whenever the equals method is overridden, so as to maintain the general contract for the hashCode method, which states that equal objects must have equal hash codes.

Then finish the testHashCodePerfect of TestSimpleOomage with code that tests to see if the hashCode function is perfect. Make sure even if the sums of the three arguments from two SimpleOomage are equal, it still fails.

@Test
public void testHashCodePerfect() {
    /* TODO: Write a test that ensures the hashCode is perfect,
      meaning no two SimpleOomages should EVER have the same
      hashCode UNLESS they have the same red, blue, and green values!
     */
    SimpleOomage ooA = new SimpleOomage(5, 10, 20);
    SimpleOomage ooA2 = new SimpleOomage(5, 10, 20);
    SimpleOomage ooB = new SimpleOomage(10, 5, 20);
    SimpleOomage ooC = new SimpleOomage(15, 5, 15);
    assertEquals(ooA.hashCode(), ooA2.hashCode());
    assertNotEquals(ooA.hashCode(), ooB.hashCode());
    assertNotEquals(ooA.hashCode(), ooC.hashCode());
}

Overide hashCode function. Since all of the arguments (red, green and blue) are multiples of 5 between 0 and 255, I divide them with 5 and represent them with power of 52(The interval is (0, 51)).

@Override
public int hashCode() {
    if (!USE_PERFECT_HASH) {
        return red + green + blue;
    } else {
        // TODO: Write a perfect hash function for Simple Oomages.
        return (int)(red / 5 + green / 5 * 52 + blue / 5 * Math.pow(52, 2));
    }
}

Evaluating the perfect hashCode

Write a utility function that returns true if the given oomages have hashCodes that would distribute them fairly evenly across M buckets. To do this, convert each oomage’s hashcode in the same way as in the visualizer, i.e. (& 0x7FFFFFFF) % M and ensure that no bucket has fewer than N / 50 Oomages and no bucket has more than N / 2.5 Oomages. The number of buckets are decided by M, so it’s fixed. Using a int[] to save the number of Oomages in each bucket will be appropriate.

import java.util.List;

public class OomageTestUtility {
    public static boolean haveNiceHashCodeSpread(List<Oomage> oomages, int M) {
        int[] bucketList = new int[M];
        for (Oomage o : oomages) {
            int bucketNum = (o.hashCode() & 0x7FFFFFFF) % M;
            bucketList[bucketNum] = bucketList[bucketNum] + 1;
        }
        for (int k : bucketList) {
            System.out.println(k);
        }
        for (int j : bucketList) {
            if ((j < oomages.size() / 50) || (j > oomages.size() / 2.5)) {
                return false;
            }
        }
        return true;
    }
}

Evaluating the perfect hashCode Visually

To get a better understanding of how hash tables work, we will use a hash table visualizer. Every item spreads out nicely because we have divided the red, green, and blue values by 5 before computing the hash code.

Compare the distribution of items for the perfect vs. imperfect hashCodes with larger M and N. We can see in the imperfect hashCode, because the red, green, and blue values are all mutiples of 5, so the sum of them is still mutiple of 5. As a result, the bucket number will always be 0, 5, 10, 15……, and the rest of the buckets will never be used.

Perfect hashCode:

Imperfect hashCode:

Evaluating the ComplexOomage hashCode

The task for this part is to write tests to find the flaw in the hashCode function of ComplexOomage. Each ComplexOomage has an entire a list of ints between 0 and 255 (not necessarily multiples of 5). This list may be of any length. For totally random ComplexOomages, everything is fine.

@Override
public int hashCode() {
    int total = 0;
    for (int x : params) {
        total = total * 256;
        total = total + x;
    }
    return total;
}

From the hashCode of ComplexOomage, we can calculate the hashcode given length of list $N$ and each argument $s$ from the function below:

From the hint.java, the last digits of powers of 256 are always 6.

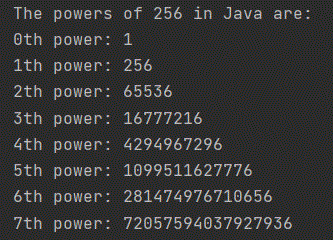
So ${s_1} \times {256^{N - 1}} + {s_2} \times {256^{N - 2}} + \ldots \ldots + {s_{N - 2}} \times 256 $ is always even, and thus the parity of the hashcode will be decided by ${s_{N - 1}} \times {256^0}$, i.e. ${s_{N - 1}}$. If the last arguments of ComplexOomages are always even or odd, the rest of buckets will never be used:

@Test
public void testWithDeadlyParams() {
    List<Oomage> deadlyList = new ArrayList<>();

    // Your code here.
    int N = 10000;

    for (int i = 0; i < N; i += 1) {
        deadlyList.add(deadlyRandomComplexOomage());
    }

    assertTrue(OomageTestUtility.haveNiceHashCodeSpread(deadlyList, 10));
}

public static ComplexOomage deadlyRandomComplexOomage() {
    int N = StdRandom.uniform(1, 10);
    ArrayList<Integer> params = new ArrayList<>(N);
    for (int i = 0; i < N - 1; i += 1) {
        params.add(StdRandom.uniform(0, 255));
    }
    params.add(0);  // The last number of the parameters decides the last digit of the hashcode, since decides the bucket number
    return new ComplexOomage(params);
}