2021 December 07 CMU15-213, C, Computer-Systems

「CMU 15-213」Lab(1) Data Lab

Environment Configuration

The labs require Linux to run test. Because installing dual system with windows can be troublesome, I instead use VMware and Ubuntu20.04 as the environment.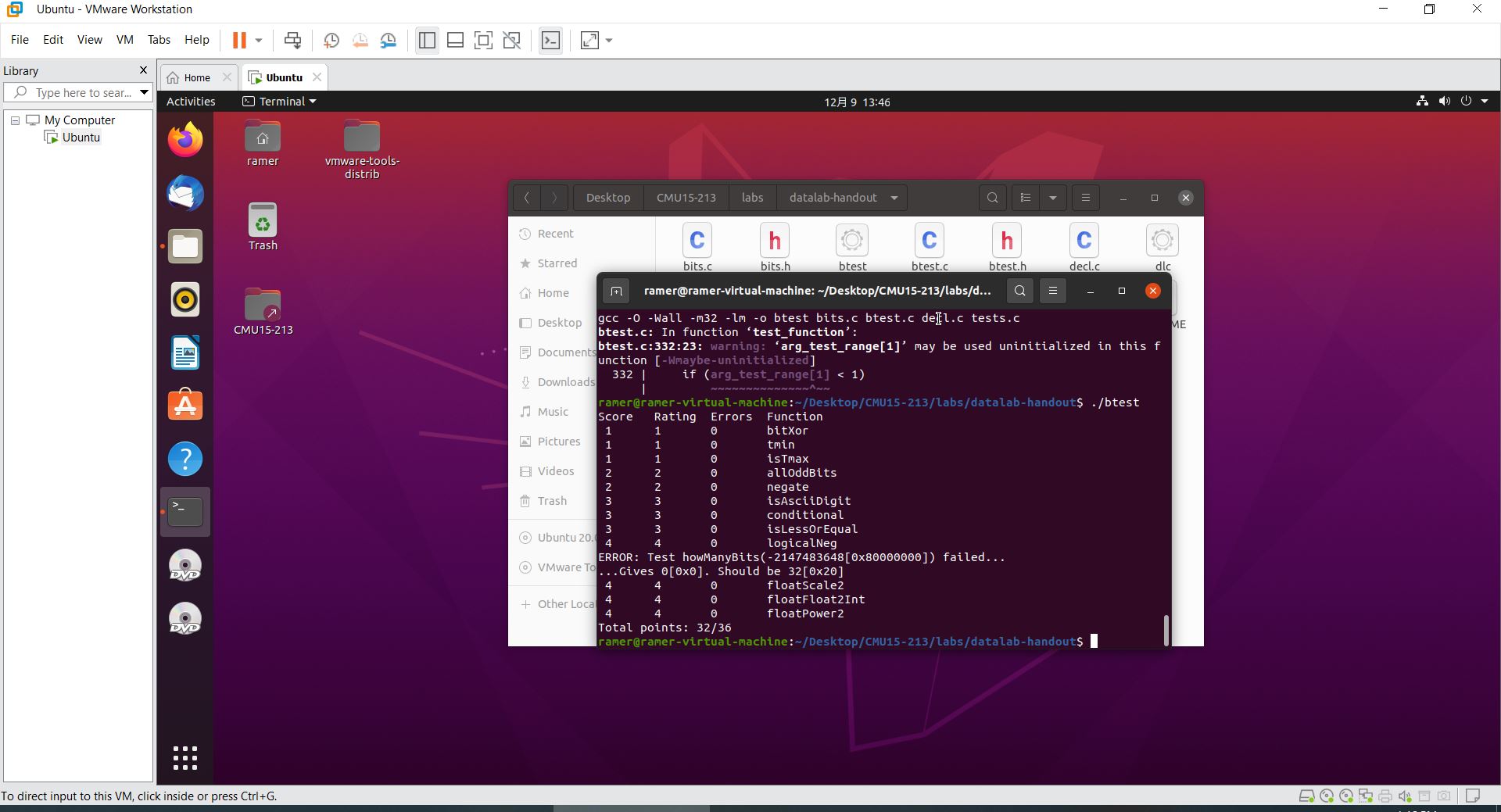

Data Lab

bitXor - x^y using only ~ and &

int bitXor(int x, int y) {
  return (~(x & y)) & (~(~x & ~y));
}

tmin - return minimum two’s complement integer

int tmin(void) {
  return 1 << 31;
}

isTmax - returns 1 if x is the maximum, two’s complement number, and 0 otherwise

I was stuck with this one for a long time because I didn’t realize “!” can be used to distinguish 0 and none-zero ints. The thought for this one is, Tmax + 1 == Tmin, and Tmax + Tmin == -1, ~(-1) == 0. But there is another situation that meets this requirement, if x = -1, ~(x + x + 1) also equals 0. So we need to make sure x + 1 not equals 0 to excude this situation.

int isTmax(int x) {
  return !(~(x + x + 1)) & !!(x + 1);
}

allOddBits - return 1 if all odd-numbered bits in word set to 1 where bits are numbered from 0 (least significant) to 31 (most significant)

Variable a is to get 0xAAAAAAAA. The operation x & a throws away even-numbered bits (set to 0). ~a is to get 0x55555555, then Xor with x & a we can get 0xFFFFFFFF if x meets the requirement.

int allOddBits(int x) {
    int a = 0xAA + (0xAA << 8);
    a = a + (a << 16);
  return !(~((x & a) ^ (~a));
}

negate - return -x

int negate(int x) {
  return ~x + 1;
}

isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters ‘0’ to ‘9’)

This one can be seperated to 2 parts. First part is from 0x30 to 0x37, all follow the pattern of 000...0110***. * means whatever number. The second part is 0x38 and 0x39, which follow the pattern of 000...011100*. So a and b represent the two parts respectively.

int isAsciiDigit(int x) {
    int a = !((x & (~0x7)) + (~0x30 + 1));
    int b = !((x & (~0x1)) + (~0x38 + 1));
  return a | b;
}

conditional - same as x ? y : z

If x == 0, a = 0. If x != 0, a = 0xffffffff.

int conditional(int x, int y, int z) {
    int a = (!x) + (~1 + 1);
  return (y & a) + (z & (~a));
}

isLessOrEqual - if x <= y then return 1, else return 0

int isLessOrEqual(int x, int y) {
    int a = (x >> 31) & (!(y >> 31)); //x<0, y>0
    int b = (!(x >> 31)) & (y >> 31);  //x>0, y<0
    int sub = x + (~y + 1);  //x-y
    int c = (sub >> 31);  //if sub < 0
  return a | (c & (!b)) | (!sub);
}

logicalNeg - implement the ! operator, using all of the legal operators except !

If x < 0 or -x < 0, a | b will be 1 (last digit). So need to reverse the result.

int logicalNeg(int x) {
    int a = x >> 31;  //if x < 0
    int b = (~x + 1) >> 31; //if -x < 0
  return ((a | b) + (~1 + 1)) & 1; //reverse the result of a | b
}

howManyBits - return the minimum number of bits required to represent x in

This one beats me. I can’t figure it out by myself.😭 Find a solution here, which is very tricky. Use shift to seperate x to two parts of length of 16 bits. Then check if high 16 bits are 0 or not. If they are, the minimum required number is less than 16. If not, the number is at least 16 and we should throw away low 16 bits by shifting right. Then we should check the low 16 bits and seperate them to two parts of length of 8 bits and so on…….

int howManyBits(int x) {
    int s, c1, c2, c3, c4, c5, c6;
    int cnt = 0;	// 	count
    s = (x >> 31) & 1;	//	sign
    x = ((s << 31) >> 31) ^ x; // If x < 0, x = ~x
    s = !!(x >> 16);	//check whether the high 16 bits have 1. If yes, s is 1
    c1 = s << 4;		//If high 16 bits have 1, the low 16 bits can count 16
    x >>= c1;		//Shift right to remove the counted bits
    s = !!(x >> 8);	//Use the length of 8 bits to check, same as above
    c2 = s << 3;
    x >>= c2;
    s = !!(x >> 4);
    c3 = s << 2;
    x >>= c3;
    s = !!(x >> 2);
    c4 = s << 1;
    x >>= c4;
    s = !!(x >> 1);
    c5 = s;
    x >>= c5;
    c6 = !!x;
    cnt = c1 + c2 + c3 + c4 + c5 + c6 + 1;	//Add all the valid bits obtained each time, then plus 1 sign bit
  return cnt;
}

floatScale2 - Return bit-level equivalent of expression 2*f for floating point argument f. Both the argument and result are passed as unsigned int’s, but they are to be interpreted as the bit-level representation of single-precision floating point values. When argument is NaN, return argument.

unsigned floatScale2(unsigned uf) {
    int exp = (uf >> 23) & 0xff;
    int s = (uf >> 31) << 31;
    int tmin = 1 << 31;
    int expPlusOne;
    unsigned c;
    if (uf == 0 || uf == tmin || exp == 0xff) {
        return uf;
    }
    if (exp == 0) {
        return ((uf + uf) & (~tmin)) + s;
    }
    expPlusOne = (exp + 1) << 23;
    c = (uf & (~(0xff << 23))) + expPlusOne;
  return c;
}

floatFloat2Int - Return bit-level equivalent of expression (int) f for floating point argument f.

int floatFloat2Int(unsigned uf) {
    int exp = (uf >> 23) & 0xff;
    int e = exp - 127;
    int eshift = 23 - e;
    int s = (uf >> 31) << 31;
    int m = uf & (~(0x1ff << 23));
    int out;
    if (exp != 0) {
        m = m + (1 << 23);
    }
    if (e < 0 || exp == 0) {
        return 0;
    }
    if (e > 30) {
        return 0x80000000u;
    }
    if (e > 23) {
        eshift = -eshift;
    }

    out = m >> eshift;
    if (s) {
        out = (~out) + 1;
    }
  return out;
}

floatPower2 - Return bit-level equivalent of the expression 2.0^x (2.0 raised to the power x) for any 32-bit integer x.

unsigned floatPower2(int x) {
    unsigned exp = 0;
    unsigned expTwo = 128;  // exponent of 2
    unsigned expHalf = 126;  // exponent of 1/2
    unsigned i;
    if (x == 0) {
        return 127 << 23;
    }
    if (x > 0) {
        exp = expTwo;
        i = 1;
        while (i < x) {
            exp = exp + 1;
            if (exp >= 255) {
                return 255 << 23;
            }
            i++;
        }
    }
    else {
        exp = expHalf;
        i = 1;
        while (i < -x) {
            exp = exp - 1;
            if (exp == 0) {
                return 0;
            }
            i++;
        }
    }
    return exp << 23;
}